Wichtig:
- Mailingliste Mathematik-Lehramt
Tragen Sie sich unbedingt ein! - Ilias-Kurs: Informationen zu Abschlussarbeiten
Modularisiertes Lehramt nach GymPO I
Vom Wintersemester 2011/12 bis 2014/15 begannen Lehramtsstudierende ihr Studium in Stuttgart im modularisierten Lehramt, einem Studiengang, der in Module aufgeteilt ist und zum Zugang ins Referendariat an Gymnasien führt.
Übergangsregelungen und Lehrveranstaltungsplanung
Zum Wintersemester 2018/19 wurde der B.Sc. auf eine neue Prüfungsordnung umgestellt, wodurch es in auslaufenden Studiengängen zu Änderungen kommt:
- Die Grundlagen der Computermathematik entfallen, stattdessen gibt es die Mathematische Programmierung, ein zweisemestriges Modul, das im Wintersemester beginnt.
- Im Wintersemester finden statt: Numerische Mathematik 1, Algebra, Mathematische Statistik
- Im Sommersemester finden statt: Topologie, Maß- und Wahrscheinlichkeitstheorie, Höhere Analysis, Numerik 2
- Statt der Geometrie kann im Aufbaubereich die Differentialgeometrie gehört werden.
Mit etwas Aufwand zusätzlich zum Studium des Lehramts mit Hauptfach Mathematik kann ein Bachelor of Science in Mathematik erworben werden. Zu beachten ist:
- Es wird empfohlen, sich spätestens im 6. oder 7. Semester für ein Parallelstudium einzuschreiben und nach Möglichkeit die Geometrie mit 9 LP prüfen zu lassen.
- Die wissenschaftliche Arbeit sollte/muss in Mathematik geschrieben werden.
- Auf Antrag kann der Prüfungsausschuss des Bachelors weitere Nebenfächer als die in der Prüfungsordnung ausdrücklich genannten zulassen. Das heißt, dass man unter bestimmten Voraussetzungen das Zweitfach oder Teile davon als Nebenfach anrechnen lassen kann.
- Für Beratungen und zu weiteren Fragen zu diesem Angebot wenden Sie sich bitte an den Studiendekan Lehramt.
- Bis zum Beginn der Vorlesungszeit des vierten Semesters ist die Orientierungsprüfung in den Hauptfächern abzulegen, diese besteht im Hauptfach Mathematik aus einem der vier Module Analysis 1, Analysis 2, LAAG 1, LAAG 2
- Bis zum Beginn der Vorlesungszeit des siebenten Semesters ist die Zwischenprüfung in den Hauptfächern abzulegen, diese ist in der Prüfungsordnung, besonderer Teil, geregelt.
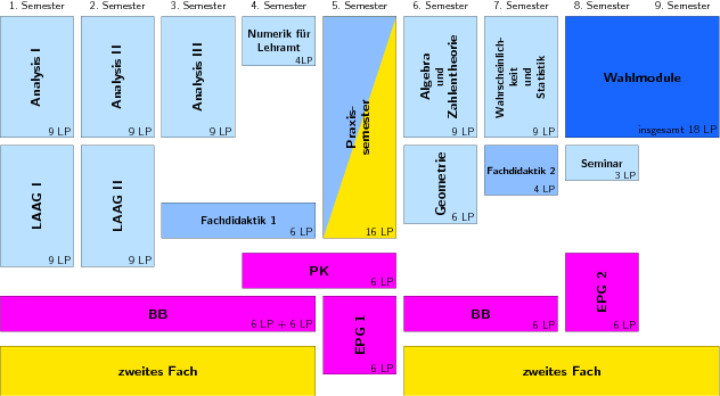
Den Aufbau der Lehramtsstudiengänge mit Mathematik als Beifach/ Erweiterungsprüfung, Künstlerisches Lehramt findet man im Regelaufbau:
- Das Vorlesungsverzeichnis ist über C@MPUS verfügbar.
- Regelaufbau der Lehramtsstudiengänge (aus der Prüfungsordnung besonderer Teil, Seite 1-7) (Download siehe unten)
- Prüfungsordnung allgemeiner Teil
- Änderungen zu den Prüfungsordnungen allgemeiner/besonderer Teil
Informationen zum Lehramt (GymPO) vom Prüfungsamt
- Laufzettel zur Wahl der Schwerpunktgebiete: Bevor Sie dem Landeslehrerprüfungsamt ihre Schwerpunktgebiete in der mündlichen Prüfung melden, füllen Sie bitte diesen Laufzettel zur Wahl der Schwerpunktgebiete aus und lassen ihn sich vom Studiendekan für das Lehramt genehmigen. Sprechen Sie bitte mit den Prüfern selbst ab, wer das Grundlagenwissen in Analysis bzw. Linearer Algebra abprüft. (Download siehe unten)
- Verordnung des Kultusministeriums über die Erste Staatsprüfung für das Lehramt an Gymnasien
(Gymnasiallehrerprüfungsordnung I -GymPO I) vom 31. Juli 2009 - Folien zur Ersten Staatsprüfung (Infoveranstaltung vom 29.1.2014) (Download siehe unten)
- Meldeformulare und Infoblätter des Regierungspräsidiums Stuttgart zur ersten Staatsprüfung unter "Erste Staatsprüfung für das Lehramt an Gymnasien (GymPO I)"
Ein Drittel der Prüfungszeit der mündlichen Prüfung im ersten Staatsexamen entfällt auf die Prüfung von Grundlagen- und Überblickswissen. Dabei können folgende Themengebiete aus den Vorlesungen Analysis und Lineare Algebra abgeprüft werden (die Nummern beziehen sich auf die Verordnung des Kultusministerium über die Erste Staatsprüfung):
2.1 Analysis:
- 2.1.1 Beweismethoden
- 2.1.2 Grenzwertbegriff
- 2.1.3 Reelle und komplexe Zahlen
- 2.1.4 Differentiation und Integration. Extremwertprobleme
- 2.1.5 Potenzreihen, rationale Funktionen, Partialbruchzerlegung
- 2.1.6 Elementare Funktionen
- 2.1.9 Potenzreihenentwicklung, Taylorformel (HF)
- 2.1.12 Elementare Differenzialgleichungen
2.2 Lineare Algebra:
- 2.2.1 Grundbegriffe der Algebra und Mengenlehre
- 2.2.2 Vektorräume und lineare Abbildungen
- 2.2.3 Matrizen, Matrixdarstellung linearer Abbildungen
- 2.2.4 Determinanten, Permutationen
- 2.2.5 Lineare Gleichungssysteme, Gauß-Algorithmus
- 2.2.6 Euklidische Vektorräume, Längen- und Winkelmessung
- 2.2.7 Geometrische Abbildungen
- 2.2.8 Eigenwerte und Eigenvektoren, Normalformen (HF)
Mit HF gekennzeichnete Gebiete gelten nur für Hauptfachstudierende.
- Prof. Dr. Uwe Semmelmann (Vorsitzender)
- Prof. Dr. Bernard Haasdonk
Downloads
Ansprechpersonen

Friederike Stoll
Dr.Studiengangsmanagerin B.Sc./M.Sc./BA-Lehramt/M.Ed. Mathematik

Jens Wirth
Prof. Dr.Studiendekan Lehramt Mathematik
[Foto: Robin Lang, 2018]

Uwe Semmelmann
Prof. Dr.Dekan der Fakultät 8Prüfungsausschussvorsitzender Lehramt Mathematik Professor - Lehrstuhl für Geometrie