Das Lehramtsstudium an der Universität Stuttgart ist aufgeteilt in ein Bachelor- und ein Masterstudium. Sie studieren zwei Hauptfächer, ergänzt durch ein bildungswissenschaftliches Begleitstudium. Auf dieser Seite finden Sie alle wichtigen Informationen zum ersten Teil, dem Bachelorstudium.
Wichtig:
- Mailingliste Mathematik-Lehramt
Tragen Sie sich unbedingt ein! - Ilias-Kurs: Informationen zu Abschlussarbeiten
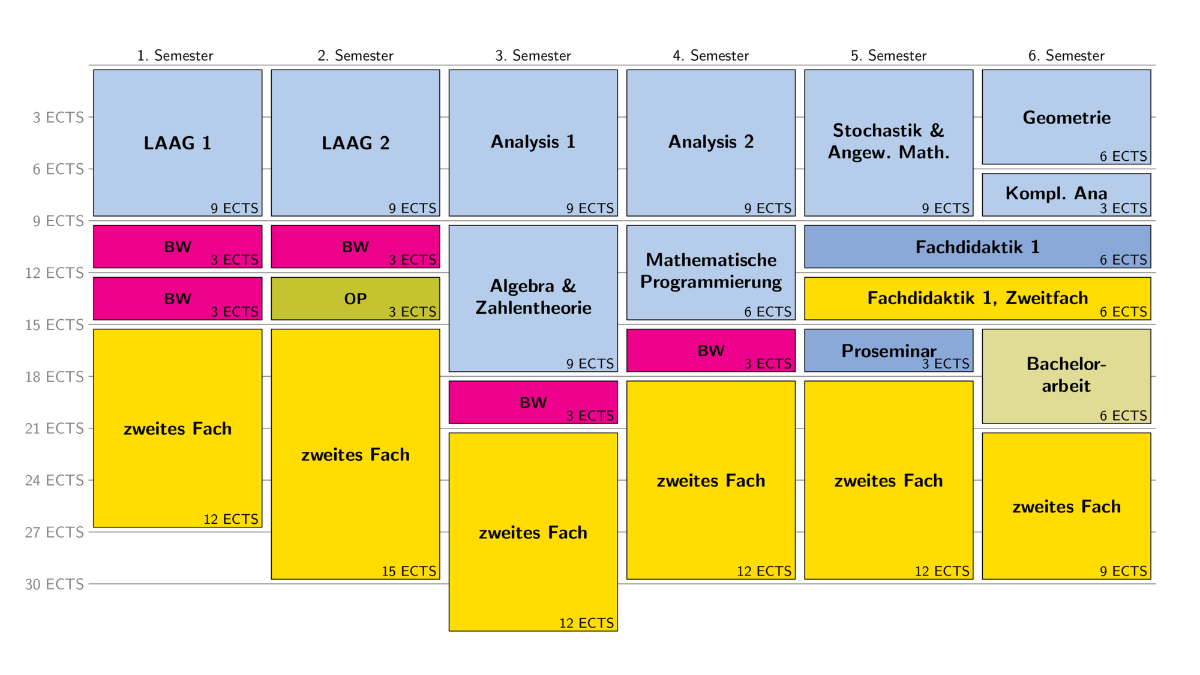
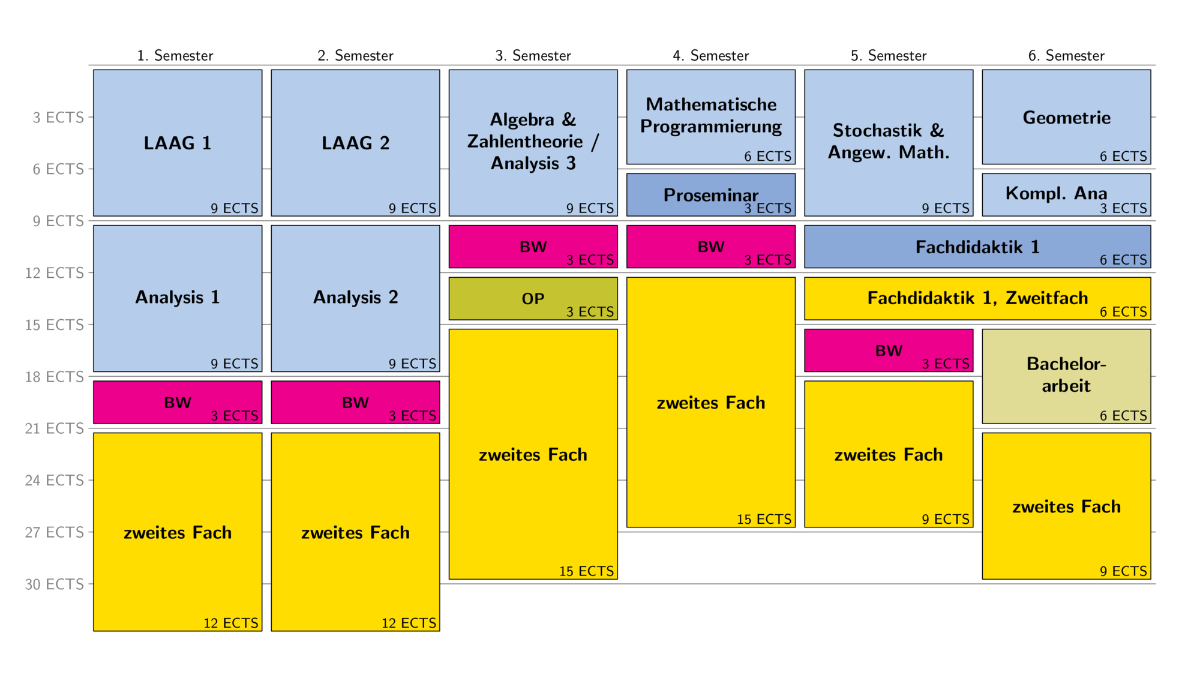
Struktur des Studiengangs
Mathematik
 |
Mathematikmodule: |
Proseminar/Fachdidaktik
 |
Proseminar und Fachdidaktik 1: |
Zweitfach
 |
Zweitfach: Neben Mathematik studieren Sie ein zweites Fach. Die Module, die Sie im Zweitfach hören, sind im besonderen Teil der Prüfungsordnung geregelt. |
BW

Bewerbung und Zulassungsbeschränkung
Ein Beginn im B.A. Lehramt Mathematik ist immer zum Wintersemester möglich. Für Bewerbungen ins Wintersemester 2023/24 war der B.A. Lehramt Mathematik nicht zulassungsbeschränkt. Der Bewerbungsschluss war daher der 15. September 2023.
- Die Orientierungsprüfung besteht aus einem der zwei Module Lineare Algebra 1 oder Analysis 1 und der Orientierungsprüfung im zweiten Hauptfach. Die Orientierungsprüfung muss bis spätestens Anfang des vierten Semesters abgelegt sein, der Erwerb des zugehörigen Scheins in den Übungen ist Zulassungsvoraussetzung zur Modulprüfung.
- Die meisten Module haben inhaltliche Voraussetzungen. Z.B. ist es sehr sinnvoll, vor der Linearen Algebra 2 die Lineare Algebra 1 und vor Analyis 2 die Analysis 1 zu hören. Auf diesen Modulen bauen die anderen Module auf. Welches die inhaltlichen Voraussetzungen für ein Modul sind, finden Sie in der Modulbeschreibung eines Moduls.
- Die Module Analysis 1, Lineare Algebra 1, Analysis 3, Algebra und Zahlentheorie und Stochastik und Angewandte Mathematik finden im Wintersemester statt, die Module Analysis 2, Lineare Algebra 2, Mathematische Programmierung, Geometrie und Komplexe Analysis (Teil der B.Sc. Vorlesung Höhere Analysis) im Sommersemester. Die Fachdidaktik 1 beginnt im Wintersemester. Das Proseminar wird jedes Semester angeboten.
- Es gibt Fristen, die Sie einhalten müssen, z.B. für die Orientierungsprüfung, Gesamtdauer, Wiederholungsprüfungen.
- In der Fächerkombination Mathematik/Physik wird in Absprache mit der Physik empfohlen, die Analysis und die Lineare Algebra in den ersten Semestern parallel zu hören. Auch bei anderen Kombinationen ist dies empfehlenswert, sofern es das zweite Fach stundenplanmäßig zulässt.
- Die Prüfungsordnung besonderer Teil
- Prüfungsordnung allgemeiner Teil, dort findet man die Regelungen, die für alle Fächer gleich gelten.
- Änderungen zur Prüfungsordnung, z.B. zu vorgezogenen Mastermodulen (Änderung vom 11.8.2017)
- Modulhandbuch in C@MPUS, dort findet man auch Modulbeschreibungen und Vorlesungstermine
- Bis spätestens zu Beginn der Vorlesungszeit des vierten Semesters muss die Orientierungsprüfung abgeschlossen sein. Die Orientierungsprüfung setzt sich zusammen aus einem der zwei Module Lineare Algebra 1 und Analysis 1 und der Orientierungsprüfung im zweiten Hauptfach.
- Die Bachelorprüfung in den Teilstudiengängen und dem bildungswissenschaftlichen Begleitstudium muss nach 10 Semestern abgelegt sein.
Teil des Bachelor-Lehramtsstudiums ist eine Abschlussarbeit in einem der beiden Hauptfächer. Mit der Bachelorarbeit erwerben Sie 6 ECTS, die Bearbeitungszeit beträgt 4 Monate. Bachelorarbeiten können von jedem/jeder Dozenten/Dozentin des Fachbereichs betreut werden. Sprechen Sie eine:n Dozenten/Dozentin selbst an und fragen nach einem Thema. Bachelorarbeiten lassen sich oft gut mit Seminaren (im B.A. dem Proseminar) verbinden.
Hilfreiche Informationen in Ilias
Zusammen mit der Fachgruppe Mathematik hat der Fachbereich einen Ilias-Kurs Informationen zu Abschlussarbeiten erstellt. Dort finden Sie Antworten auf häufige Fragen, Steckbriefe der Betreuer:innen sowie Latex-Vorlagen.
Verwendung von IT-/KI-gestützten Schreib- und Programmierwerkzeugen
Was Sie bei der Verwendung von IT-/KI-gestützten Schreib- und Programmierwerkzeugen beachten müssen, finden Sie in der Handreichung der Fakultät Mathematik und Physik.
Mit etwas Aufwand zusätzlich zum Studium des Lehramts mit Hauptfach Mathematik könenn Sie einen Bachelor of Science in Mathematik erwerben. Zu beachten ist:
- Module, die gemeinsam mit Studierenden des Bachelor of Science gehört werden, werden dabei direkt angerechnet. Einige der Lehramtsmodule sind im Bachelor of Science als Wahlmodule wähl- und anrechenbar, während einige der Wahlkernmodule aus dem Fachbachelor auch als Lehramtsmodule anerkannt werden können.
- Unter bestimmten Voraussetzungen können Module aus dem Zweitfach als Ergänzungsmodule im Bachelor of Science angerechnet werden.
- Für Beratungen und zu weiteren Fragen zu diesem Angebot wenden Sie sich bitte an den Studiendekan Lehramt oder den Polyvalenzbeauftragten des Fachbereichs Mathematik.
- Prof. Dr. Uwe Semmelmann (Vorsitzender)
- Prof. Dr. Jens Wirth (Stellvertretender Vorsitzender)
- Prof. Dr. Bernard Haasdonk
Ansprechpersonen

Friederike Stoll
Dr.Studiengangsmanagerin B.Sc./M.Sc./BA-Lehramt/M.Ed. Mathematik

Jens Wirth
Prof. Dr.Studiendekan Lehramt Mathematik
[Foto: Robin Lang, 2018]

Uwe Semmelmann
Prof. Dr.Dekan der Fakultät 8Prüfungsausschussvorsitzender Lehramt Mathematik Professor - Lehrstuhl für Geometrie